强化学习中的Terminated 和 Truncated

深度强化学习的流程可以抽象为以下步骤的重复：

1. 智能体与环境交互产生并存储经验
2. 智能体从经验中进行学习

本文主要探讨在收集经验过程中，环境自然结束（Terminated，包括目标成功，失败等）和人为截断（Truncated，主要为达到一定步数结束）对经验收集和训练产生的影响，以及如何对其进行处理。并对其进行了部分实验来比较性能。

Q-Learning 简介

在Q-Learning系列算法中，智能体要学习估计每个状态$s$下每个动作的最优Q值$Q^{\ast }(s,a)$。其贝尔曼方程如下： $$\begin{array}{}\text{(1)}& Q^{\ast }(s_t,a_t)=r_t+\gamma \cdot \underset{a^{\prime }\in A(s_{t+1})}{max}{Q}^{\ast }(s_{t+1},a_{t+1})\end{array}$$ 而当$s_{t+1}$为一局的结束状态，即$done(s_{t+1})=True$时， $$\begin{array}{}\text{(2)}& Q^{\ast }(s_t,a_t)=r_t\end{array}$$

写在一起为： $$\begin{array}{}\text{(3)}& Q^{\ast }(s_t,a_t)=\{\begin{array}{lr}{r}_t+\gamma \cdot \underset{a^{\prime }\in A(s_{t+1})}{max}{Q}^{\ast }(s_{t+1},a_{t+1})& ifdone(s_{t+1})=False\\ r_t& ifdone(s_{t+1})=True\end{array}\end{array}$$ 在程序实现过程中，通常写为：

q_target = reward + self._gamma * max_next_q_value * (1 - done)

截断问题

Q-Learning的关键在于对于值函数的准确估计，如果环境在推演过程中被人为截断，如果被当作环境终止来处理，则对$Q^{\ast }$的估计就少了一项$\gamma \cdot \underset{a^{\prime }\in A(s_{t+1})}{max}{Q}^{\ast }(s_{t+1},a_{t+1})$。这在一定程度上会使$Q^{\ast }$函数在学习的过程中不稳定，或难以收敛。另外，终止状态往往和奖励$r_t$有关，若不对人为截断的情况进行另外处理，则有可能会给智能体一个有偏差的奖励，从而使智能体的训练过程出现问题。

因此，在经验记录和reward设计时，除了要考虑环境自然结束（Terminated）外，也要考虑提前终止等人为截断（truncated）的情况。强化学习环境库gym从0.26版本开始，每个step都会返回这两个信息，从而方便训练。

考虑截断的情况下，$Q^{\ast }$的贝尔曼方程的程序实现就变为了：

q_target = reward + self._gamma * max_next_q_value * (1 - done + truncated)

实验对比

本文在gym的CartPole-v1环境上进行测试，最大回合数设为200，训练步数为500，隐层网络为2层64节点的全连接网络，每步训练次数为8，buffer size为100000，batch size为64，最小训练经验数为500，初始$ϵ=0.9$，终止$ϵ=0.01$，$ϵ$ decay 步数为200步，奖励函数为：

def cart_pole_v1(params):
    reward = params["reward"]
    step = params["step"]
    done = params["done"]
    truncated = params["truncated"]
    if done and (not truncated):
        return -100
    else:
        return 1/((step+1)**2)

在DQN算法中实验结果如图1所示：

图1 DQN对比

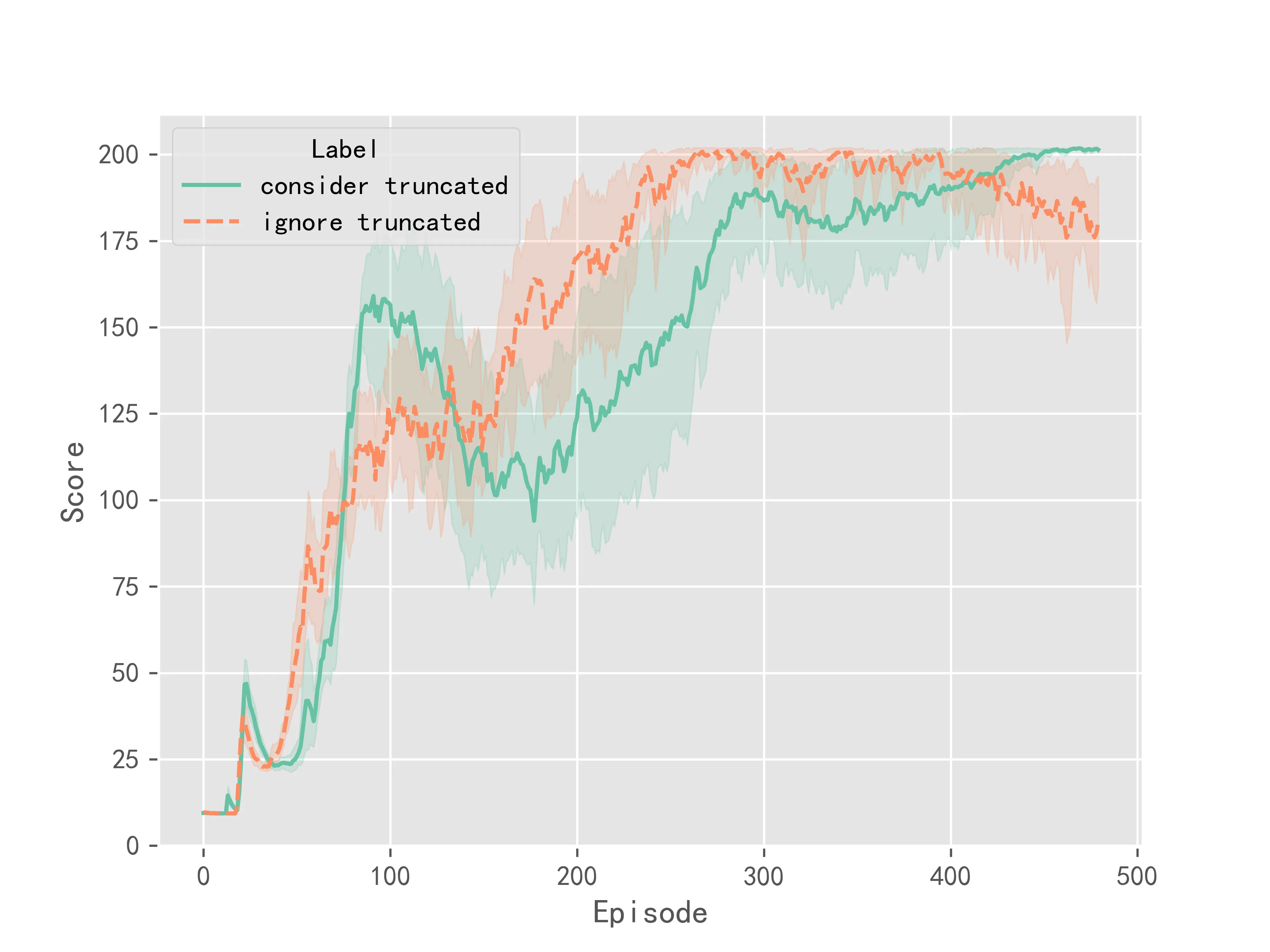
在Double DQN算法中实验结果如图2所示：

图2 DoubleDQN对比

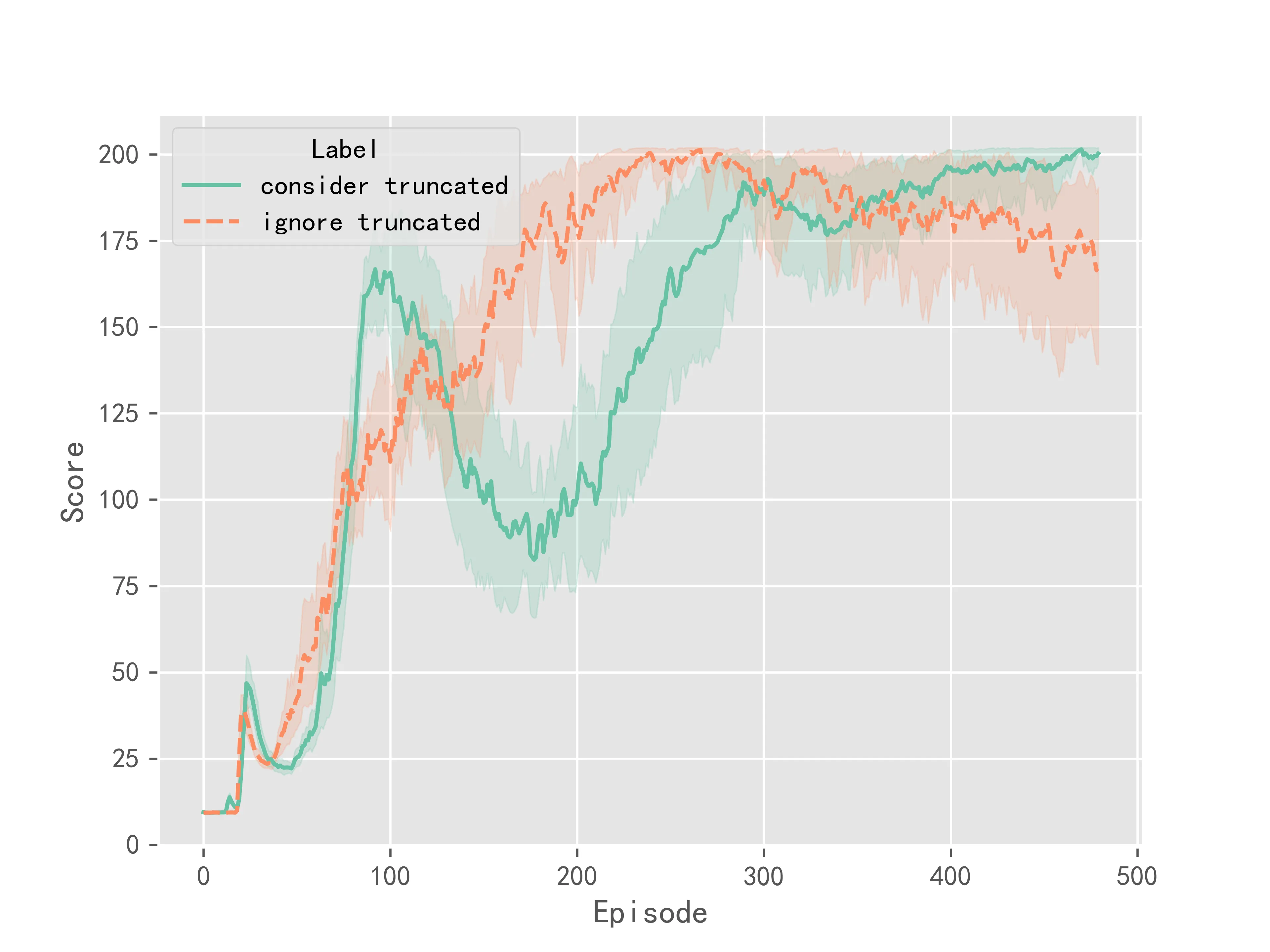
在Dueling DQN算法中实验结果如图3所示：

图3 DuelingDQN对比

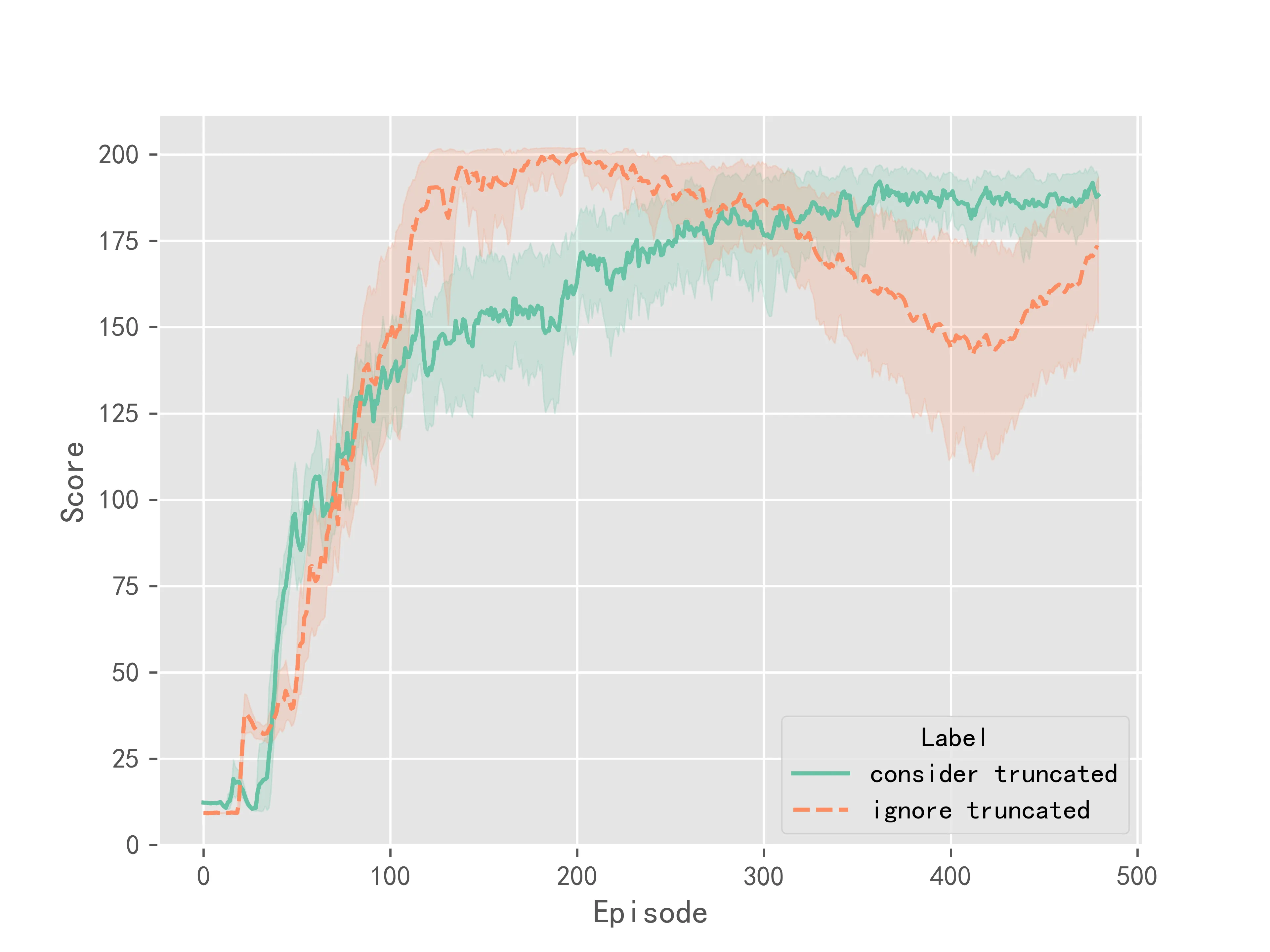
在D3QN算法中实验结果如图4所示：

图3 DoubleDuelingDQN对比

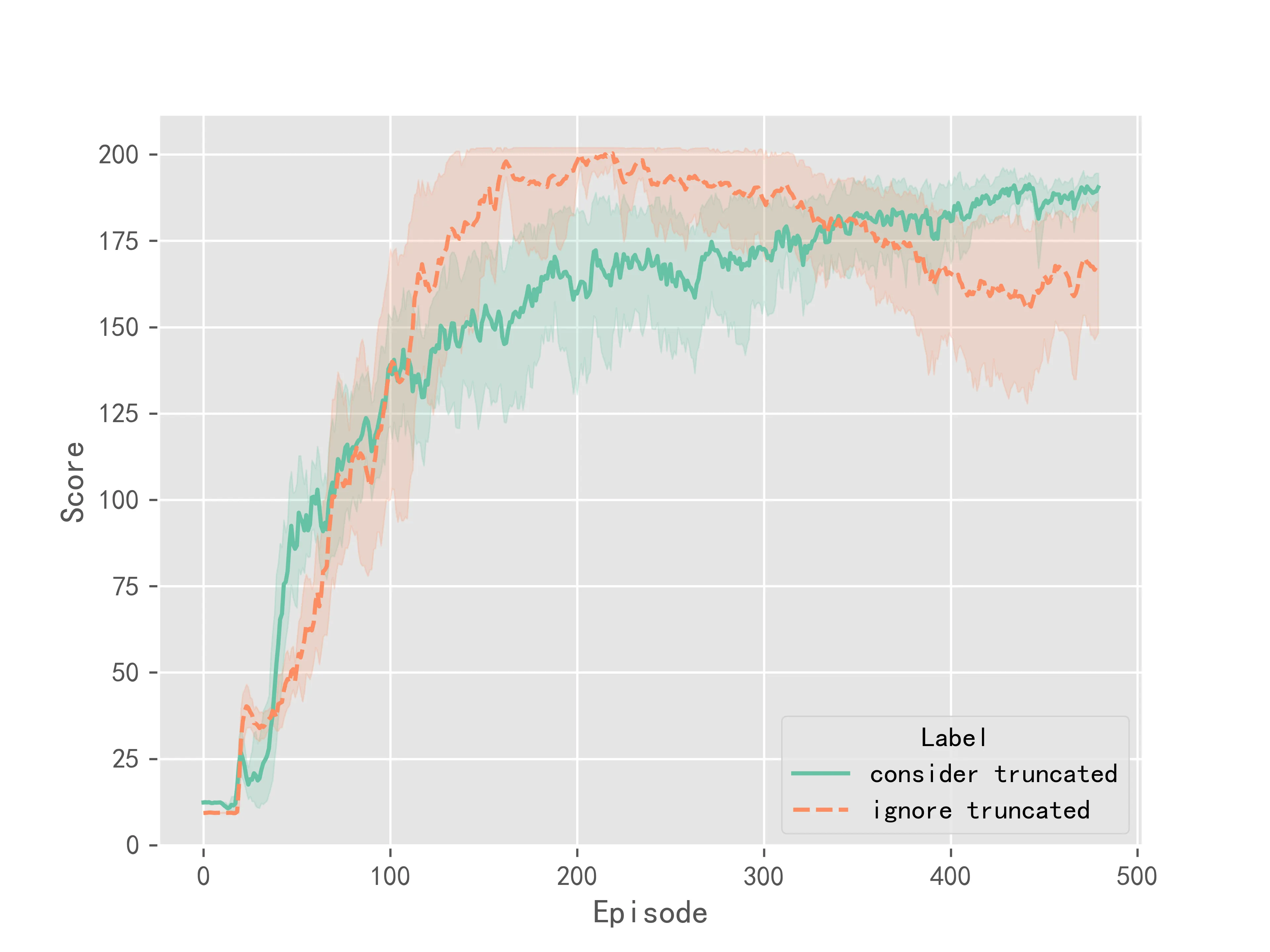
上述实验结果表明，相比于不考虑截断，考虑截断情况之后，算法的训练更加稳定，最终收敛的结果方差较小。但考虑截断并不能明显提升Q-Learning系列算法的收敛速度或是表现性能。它更多的是提升了训练时的稳定性。