黄蜂群算法改进的多机器人区域覆盖

GitHub地址：https://github.com/KezhiAdore/MultiRobots_CoverMap

码云地址：https://gitee.com/KezhiAdore/MultiRobots_CoverMap

一、问题提出

1. 背景

机器人在工业、国防和科学技术中的应用日益广泛， 它能够在枯燥和危险的复杂非结构化环境下工作。使用机器人大大提高了人们的工作效率， 改变了人们的生活方式， 带来了巨大的经济和社会效益， 有力地推动了有关学科和技术领域的发展。

区域覆盖是指携带有一定探测范围的传感器如激光、声纳等的机器人探索访问整个区域， 并完成相应任务的过程。区域覆盖是自主移动机器人的一项基本任务。

图1.1 扫地机器人——机器人区域覆盖问题的一个实例

2. 问题定义：

1. 一群有自主移动能力和有限感知能力的机器人，协作对有界联通区域进行覆盖。

2. 机器人可重复覆盖区域中的某一位置，目标是区域的覆盖率到达一定值。

3. 机器人以分布式的，非集中控制的方式完成任务，依据自身探测到的局部信息确定行动逻辑，不依赖于外部的控制。

4. 要求覆盖的速度尽可能快。

3. 问题的复杂性分析

相对一般的智能优化问题，群机器人区域覆盖问题在以下方面更加复杂：

• 动态性：加入了时间维度，问题所得到的解是若干个机器人行走的路径（点序列），解空间极其庞大。

• 分布式：算法的执行中心在单个的机器人上，没有外部主机予以统一控制。而单一机器人的计算能力和感知能力不高，用以决策的算力与信息有限。

• 大规模：为了保证地图表示的精度，栅格地图的单元格数必然很多。同时实际环境地图复杂多变且面积较大，机器人数目较多。

二、模型初步建立

1. 对环境的建模

将地图栅格化，形成栅格地图作为机器人运动和障碍物放置的环境。

栅格地图是把环境划分成一些矩形的小栅格，其中每一栅格作为机器人运动，覆盖的最小单元。每个栅格都具有一定的属性，例如信息素的浓度，是否被覆盖过，以及是空地或是障碍物。

图2.1 栅格化示例

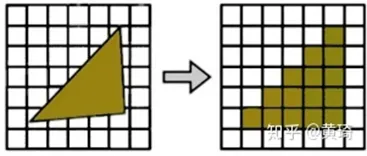
在地图中遍布有一些障碍物，对于障碍物栅格，机器人不能通过，但是可以被机器人感知到。

2. 对机器人的建模

2.1机器人质点化

忽略机器人的物理形态，把机器人当作一个无体积无碰撞的质点。机器人只能处于栅格地图中某一个单元格内，同一单元格允许存在有多个机器人。

2.2机器人探测范围

由于分布式机器人电源的局限性，其探测范围也是很有限的，在栅格化地图上为了简化运算，将机器人的探测信息素的范围规定为上下左右四个单位。

图2.2 机器人的探测范围

2.3机器人的功能

机器人可以执行以下操作：移动到上下左右四个方向中的一个或者保持不动，对上下左右和本身所处的单元格进行感知，以及对自身所处的单元格的信息素浓度进行修改。

我们更多地考虑信息素对于机器人行为的影响而不是研究在物理上具体使用什么信息素来通信，因此将每个位置的信息素浓度抽象为一个数字，机器人到达该位置即可以修改该地的信息素。

3.对时间的建模

将时间离散化，每一单位时间称为“轮”。每一轮，每个机器人按照以下流程进行行动：

Step1：实现对当前单元格的覆盖

Step2：修改当前所在单元格的信息素

Step3：进行一次移动，或者选择停在原地不移动。

每轮所有机器人这三步行为都是同步发生的。

4.对问题的解的建模

4.1解的表示

对于一个单元格，可以使用横纵坐标组成数对$(x,y)$来表示。那么假如覆盖过程持续了$t$轮，共有$n$个机器人参与覆盖，解可以由$n$个长度为$t$的单元格序列表示，即每个机器人的移动轨迹。其中合法的解不应该包含有障碍物单元格。所有单元格组成的集合，就是已覆盖的单元格。

4.2解的优劣衡量

我们定义覆盖率为已被覆盖的单元格在所有单元格中的占比。同时设定，目标覆盖率为$\alpha$。当前覆盖率超过$\alpha$或时间超过上限之时，覆盖过程停止。解的优劣由覆盖用时$t$衡量。对于相同大小的地图，同样数目的机器人，达到给定覆盖率的用时越短则解越好。进行多次试验。达到给定覆盖率的平均用时越短则算法性能越好，平均用时的标准差越小说明算法性能越好。

三、算法设计及改进

1. 地图和机器人共性描述

针对该问题，不同的覆盖算法机器人的运行规则不同。但是地图的建立和描述在不同算法中是相同可以复用的。对于地图的描述如下： - 地图大小为$M\ast N$，机器人总数量为$n$，分别为$r_1,r_2\dots r_i\dots r_n$ - 地图上某一点$(i,j)$的信息素为$s_{ij}$，初始时每个点的信息素为1

2. 基本的黄蜂群算法

机器人的运行规则为：

1. 每个机器人的响应阈值为: $\theta$
2. 对于处在$(x_i,y_i)$的机器人$r_i$，首先更新其所在位置的信息素：

$$\begin{array}{}\text{(1)}& s_{x_i{y}_i}=s_{x_i{y}_i}\ast \alpha （\alpha \in (0,1)）\end{array}$$

3. 探测四周的信息素记为：上：$s_1$ 下：$s_2$ 左：$s_3$ 右：$s_4$

4. 机器人选择方向$k$的概率为： $$\begin{array}{}\text{(2)}& \frac{s_k^2}{{\theta }^2+\sum _{k=1}^4{s}_k^2}\end{array}$$

5. 停留在原地的概率为： $$\begin{array}{}\text{(3)}& \frac{{\theta }_i^2}{{\theta }^2+\sum _{k=1}^4{s}_k^2}\end{array}$$

6. 使用轮盘赌法选择下一步的运动方向或是停留在原地

上述算法是文献中最基本的黄蜂群算法，有两个影响机器人运行的参数$\theta$和$\alpha$，通过仿真实验分别探究这两个参数对于地图覆盖的影响。以下所有仿真地图大小为$100\ast 100$，机器人数量为50，初始随机分布地图上。

图3.1 θ的变化对于覆盖结果的影响

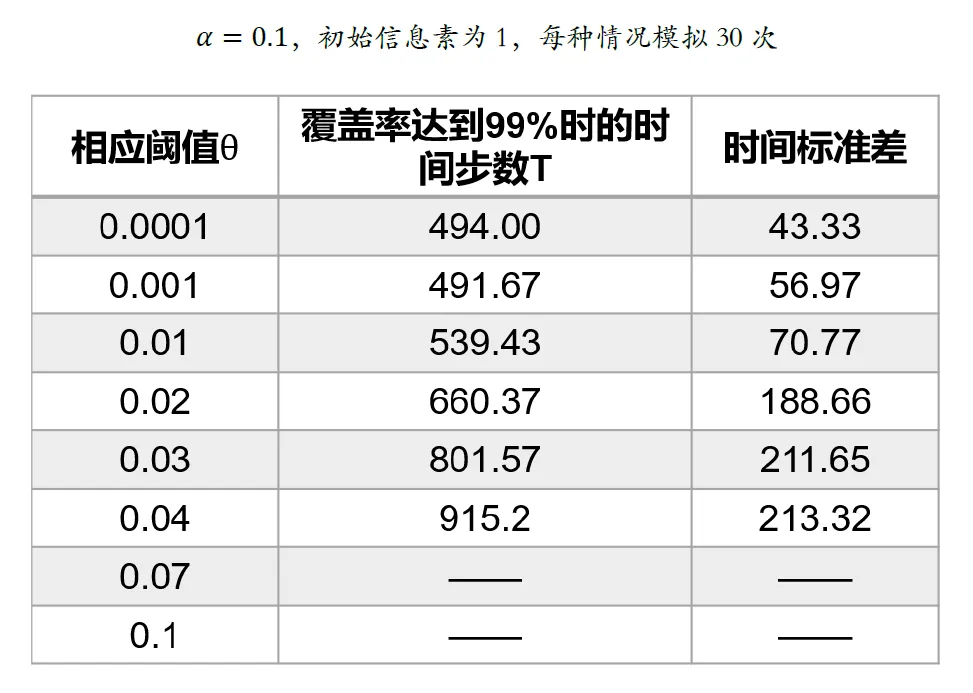
从上述实验结果可以看出，随着$\theta$的增加，覆盖时间和时间方差迅速增长，从算法角度分析，$\theta$越大，机器人在四周被探索之后有更大的角度停留在原地。

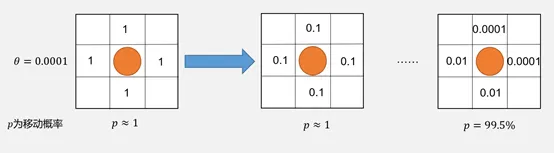
在$\theta$很小时，即使机器人当前四周的方格被经过了多次，机器人仍有很大的概率继续移动，而非停留在原地。

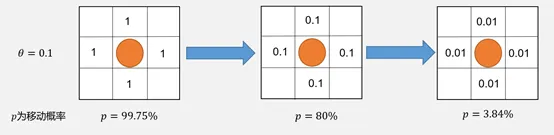
当$\theta$相较于初始信息素相差不大时，如上图，$\theta$为初始信息素的1/10，在这样的情况下，如果其周围的四个方格均已被访问两次以上，则其移动的概率大大降低。这就导致覆盖时间均值和方差急剧上升。 结合上述实验结果，再结合现实实际情况进行考量，由于$\theta$在取得较小时机器人停留在原地的作用已经微乎其微，而$\theta$较大时又会严重影响地图覆盖速度，而在实际应用场景中，我们更希望群机器人以很快的速度完成覆盖而非节省能源。因此，我们选择去掉机器人停留在原地的规则，即$\theta$=0。 在经过上述变动之后，再进行实验探究$\alpha$变化对于群机器人覆盖时间的影响。

图3.2 α的变化对于覆盖结果的影响

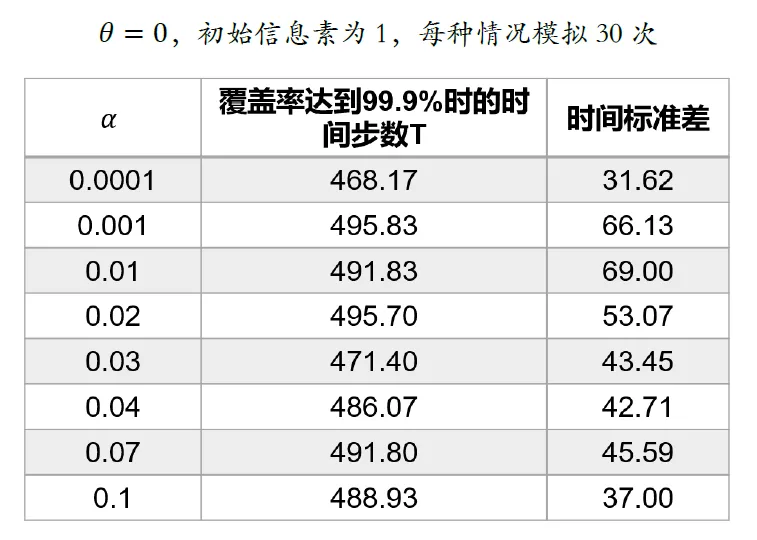
由上述实验数据可以看出，随着$\alpha$的变化，覆盖时间和覆盖时间标准差变化不大，并且有着先增大后减小的趋势。这是因为在$\alpha$很小时，探索过区域的信息素浓度变化很快，有效的防止了重复探索，而在$\alpha$较大时，对于回到曾经探索过的区域有一定的容忍，可以让机器人回到原来区域覆盖之前漏掉的区域。两者各有优劣，不过总的来说，$\alpha$的取值对于覆盖效率的影响不大。

3. 自适应信息素释放黄蜂群算法

对上述黄蜂群算法进行分析，我们发现，以下两种情况在黄蜂群算法下，中心区域信息素的变化是相同的。

图3.3 地图探索的不同情形

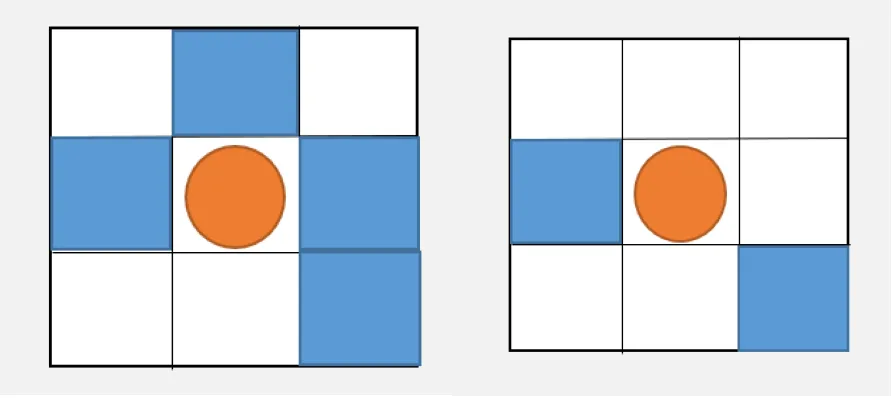
但实际上，对于右图，为了探索中心节点周围的空白节点，我们希望有机器人可以再次回到中心节点。而对于左图，由于其四周基本都已经被探索完全，再次回到中心节点的意义不大，我们希望机器人尽量不要回到该区域。 由此，我们提出自适应释放信息素的方法，当周围未探索方格较多时，信息素的修改较小，当未探索方格较多时，信息素的修改较大。同时我们希望该变化是非线性的，新的信息素释放方法如下：

• 信息素的基本更新依然为： $$\begin{array}{}\text{(4)}& s=s\ast \alpha \end{array}$$
• 设某个方格周围的空格格数为m个，则增加的权重指数为: $$\begin{array}{}\text{(5)}& k=1+\frac{4-m}{4}\end{array}$$
• 那么机器人在某个方格更新信息素的方式变为： $$\begin{array}{}\text{(6)}& s=s\times {\alpha }^k\end{array}$$

4. 有记忆回溯的黄蜂群算法

在障碍物地图覆盖测试中，我们发现，会出现如下现象：机器人困在某个入口很小的封闭小区域无法出门。这就导致机器人被困住无法正常工作。

图3.4 机器人被困

为了避免这种情况，我们考虑到深度优先搜索具有的回溯性特点，通过记忆历史路径在无路可走时进行回溯，结合记忆回溯黄蜂群算法的算法流程如下：

图3.5 记忆回溯黄蜂群算法

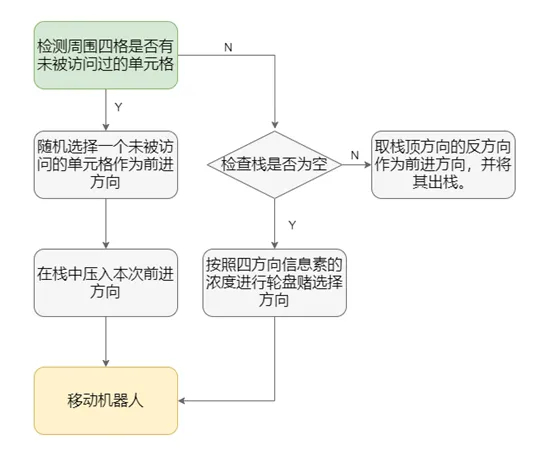
使用该算法便可以使机器人即使进入局部障碍物区域，也可以通过记忆路径回溯从局部环境走出，具有很好的可靠性和鲁棒性。

四、性能测试及改进方向

1.空旷地图测试

空旷地图是最简单，最方便测试的地图，在其上的测试结果可以很好的反映上述几个算法耗费的时间以及时间稳定性。同时本次实验加大实验次数，每张地图每种算法测试500次，避免偶然性，在空旷地图上的测试结果如下：

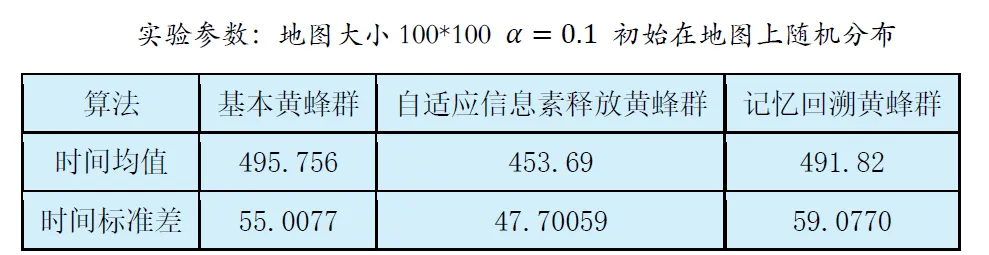
由上述实验结果可以看出，自适应信息素释放黄蜂群的探索时间最短，时间稳定性也最好，其他两个算法覆盖时间相当，时间稳定性记忆回溯黄蜂群略差。

2. 简单障碍物地形测试

图4.1 简单障碍物地图

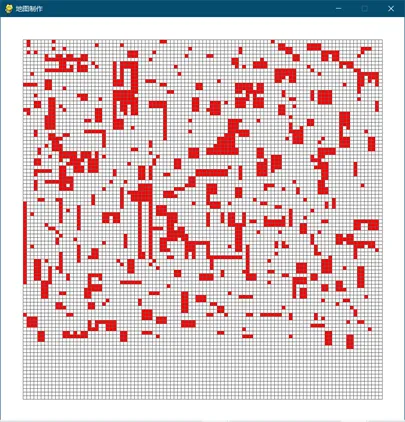
在上述地图的测试结果为：

测试结果与在空旷地图中的结果有了很大的不同，记忆回溯黄蜂群的两个评价指标最优，其次是自适应信息素释放的黄蜂群，基本黄蜂群所花费的时间较长，时间稳定性也较差。

3. 实地地形测试

3.1 温泉浴室

温泉浴室的地图如下：

图4.2 温泉浴室平面图

该地图最大的特点是存在大量的小房间，入口很小，机器人进入之后很容易被困住无法出来，在该地图上三种算法的运行结果为：

由于地形的影响，加之为了测试实际环境，所有机器人均从地图左上角出发而非初始随机分布，使得三种算法覆盖地图所用时间有了较大延长。

三项结果对比，记忆回溯黄蜂群的运行效率最高，自适应信息素释放黄蜂群效率次之并且相差不大，而基本黄蜂群所用的时间较长且时间稳定性差。

3.2 仲英书院

仲英书院的地形如下：

图4.3 仲英书院平面图

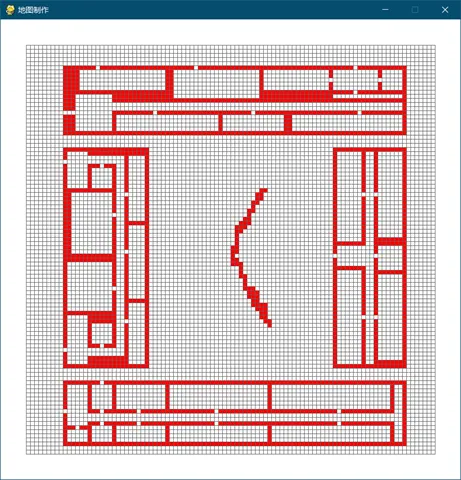
实验结果为：

在此地图中，记忆回溯黄蜂群明显由于其余两个智能算法，自适应信息素释放也同样比基本的黄蜂群算法时间效率上更优，时间稳定性上，记忆回溯黄蜂群的优势相比其余两个优势很大。

4. 实验结论

• 启发式信息素释放的黄蜂群算法相较于基本的黄蜂群算法在全部情况下时间花费更优。

• 深度优先搜索改进的黄蜂群算法在空白地图上优势不大，甚至在同一起点出发时效果很差，但在有大量障碍物的地图上表现很好，由于基本黄蜂群算法和启发式黄蜂群算法。

5. 其他改进思路

有限长度记忆的深度优先搜索改进的黄蜂群算法

由于实际情况下，无限记忆的dfs算法会因为移动误差和内存限制原因而难以实现，可以在算法中加入长度限制。

1. 队列限长：使用双端队列替代栈，在队列长度超出限制时弹出队尾元素。
2. 栈限长：在栈长度超出限制时强制回溯。