BP神经网络

发表于 更新于 分类于 阅读次数： Waline： 本文字数： 2.2k 阅读时长 ≈ 2 分钟

BP神经网络概述

BP神经网络是神经网络中最基础也是应用最多的神经网络，它由三层节点组成，分别为输入层，隐含层和输出层。BP神经网络的实现比较简单，主要分为正向传递输出和反向传递误差两部分。

神经网络的万能逼近定律：一维阶梯函数的线性组合可以逼近任何一维连续函数；sigmoid函数可以逼近阶梯函数，因此一维sigmoid函数的线性组合能够逼近任何连续函数。（1989年，Robert Hecht-Nielsen）这为神经网络的应用提供了理论依据。

神经网络的优点就在于，很多我们很难去求解的函数映射关系，可以通过对多个一维阶梯函数组合得到，那么如何对这些一维函数进行组合就成了神经网络建立的主要问题和难点。

BP神经网络认识

BP神经网络可以看做是一个多输入多输出的函数，如果不考虑内部结构，它的黑盒模型如下：

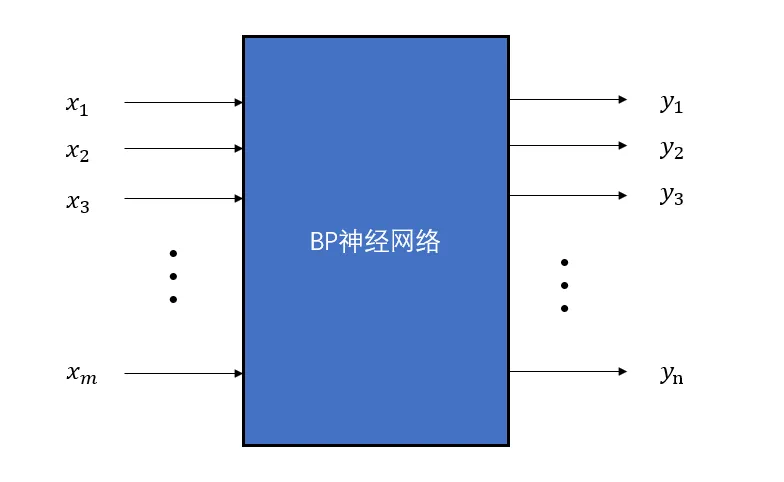
BP神经网络的黑盒模型

在该BP神经网络中，输入为\(m\)个，输出为\(n\)个，我们知道输入和输出之间应当还有一层隐含层，那么隐含层的节点个数应当如何选取。一般来说，隐含层的确定由如下的经验公式所决定： \[ h=\sqrt{m+n}+a \] 其中\(h\)为隐含层节点数目，\(m\)为输入层节点数目，\(n\)为输出层节点数目，\(a\)为之间的调节常数

那么根据输入和输出的节点数，我们就可以构造一个简单地BP神经网络模型了，它的内部结构如下（以\(m=3,n=3,h=3\)为例）：

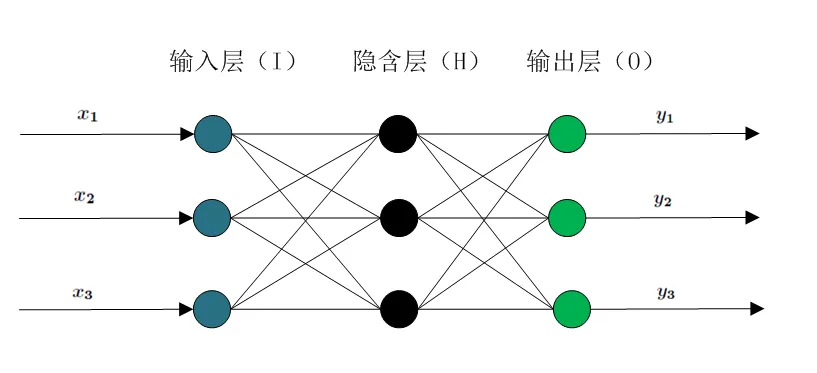
image-20200422003732195

这样的一个三层的神经网络就可以通过一维函数的组合来实现任意的3维到3维的映射，那么如何建立这种映射呢？，这个问题其实就是如何对BP神经网络进行训练。训练的过程主要分为两部分：前向传递结果，反向传递残差。

前向传递

对于BP神经网络中的任何一个节点，其输入为上一层节点输出的加权和，以隐含层为例，设输入层节点的输出为\(x_i\)，隐含层节点的输入为\(net_j\)，输入层的节点\(i\)连接到隐含层节点\(j\)的权值为\(w_{ij}\)，常数项为\(b_j\)则隐含层节点的输入为： \[ net_j=\sum_{i=1}^m w_{ij}x_i+b_j \] 在BP神经网络中，为了保证激活函数处处可导，选用sigmoid函数作为激活函数，那么节点输出为： \[ f(net_j)=\frac1{1+e^{-net_j}} \]

使用sigmoid的优点：

  1. 相比于阶梯函数，它在定义域上处处可导
  2. 令\(y=sigmoid(x)，则y^,=y(1-y)\)。可以看出sigmoid函数的导数可以用自身来表示。这样，一旦计算出sigmoid函数的值，计算它的导数的值就非常方便。这为后面反向传播时使用梯度下降法提供了便利。

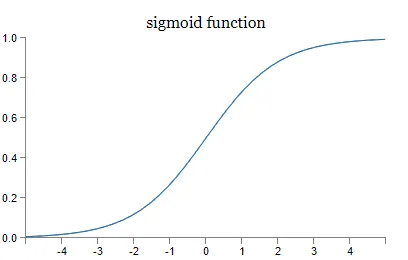
Sigmoid 函数的主要缺陷：

  1. 梯度消失： 注意：Sigmoid 函数趋近 0 和 1 的时候变化率会变得平坦，也就是说，Sigmoid 的梯度趋近于 0。神经网络使用 Sigmoid 激活函数进行反向传播时，输出接近 0 或 1 的神经元其梯度趋近于 0。这些神经元叫作饱和神经元。因此，这些神经元的权重不会更新。此外，与此类神经元相连的神经元的权重也更新得很慢。该问题叫作梯度消失。因此，想象一下，如果一个大型神经网络包含 Sigmoid 神经元，而其中很多个都处于饱和状态，那么该网络无法执行反向传播；

  2. 不以零为中心： Sigmoid 输出不以零为中心的；

  3. 计算成本高昂： exp() 函数与其他非线性激活函数相比，计算成本高昂。

sigmoidal函数

每个神经元进行这样独立的运算，那么对于一组输入，神经网络就可以进行运算得到相应的输出。这就是前向传递的过程。

反向传递

在初始时，系统中的所有权值时随机确定的。因此要通过学习训练数据，不断地修正节点中的权值来使得模型趋向于我们希望的结果。反向传递的基本算法思想是非线性规划中的梯度下降算法，规划的目标为最小化损失函数。大体流程如下：

  • 设定损失函数，假设输出层的所有结果为\(d_j\)，则损失函数如下：

\[ E(w,b)=\frac12\sum_{j=0}^{n-1}(d_j-y_j)^2 \]

  • 通过损失函数修正隐层到输出层的\(w、b\)进行修正。对于隐层的节点\(i\)到输出层节点\(j\)的权值\(w_{ij}\)，进行如下修正（其中\(\eta\)为学习率）：

\[ \Delta w=-\eta\frac{\partial E}{\partial w_{ij}} \]

  • 同样的，对于\(b\)的修正为：

\[ \Delta b=-\eta\frac{\partial E}{\partial b_{i}} \]

基本上就是这么个思路，求偏导的过程比较复杂这里就不展开说了，记住梯度下降法最小化损失函数的思想就可以了。

参考文献

[1]ACdreamers. BP神经网络[G/OL]. CSDN: 2015.03.26[2020.04.22]. https://blog.csdn.net/acdreamers/article/details/44657439

[2]东皇Amrzs. [整理] BP神经网络讲解——最好的版本[G/OL]. 简书: 2017.02.28[2020.04.22]. https://www.jianshu.com/p/3d96dbf3f764

[3]lx青萍之末. BP神经网络[G]. CSDN: 2018.07.20[2020.04.22]. https://blog.csdn.net/daaikuaichuan/article/details/81135802